What is HCF?
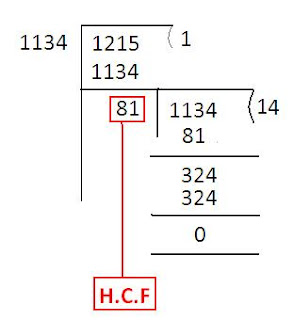
HCF and LCM > Important Formulas( HCF ) Highest Common Factor( HCF ) Highest Common Factor( HCF ) of two or more numbers is the greatest number which divides each of them exactly. Greatest Common Measure(GCM) and Greatest Common Divisor(GCD) are the other terms used to refer HCF . If you want to buy a book of HCF click here - CLICK Highest Common Factor(HCF) Highest Common Factor(HCF) of two or more numbers is the greatest number which divides each of them exactly. Greatest Common Measure(GCM) and Greatest Common Divisor(GCD) are the other terms used to refer HCF. Example : HCF of 60 and 75 = 15 because 15 is the highest number which divides both 60 and 75 exactly. We can find out HCF using prime factorization method or by dividing the numbers or division method. Example 1: Find out HCF of 60 and 75 Step 1 : Express each number as a product of prime factors. 60 = 2 2 × 3 × 5 75 = 3 × 5 2 Example 2: Find out HCF of 36, 24...
